2025年辽宁省考行测技巧：“标数模型”巧解换乘问题
在行测数量关系中，排列组合问题一直是困扰大家的一大难题，而其中的公车换乘问题因涉及多种换乘方式，同学们在做题时总是多算或者少算，容易出错。今天小编就为大家带来一种模型巧解这类问题。
一、基本概念
标数模型是指在求最短路径的过程中，在地图上所有的路口处标出到此路口的线路总数，从而求出到终点最短路径数的一种方法。
二、具体步骤
1.确定方向
2.找准来路
3.依据末路等于来路之和逐一标数
三、模型展示
【例1】如图所示，求A点到B点的最短路径数有几条?
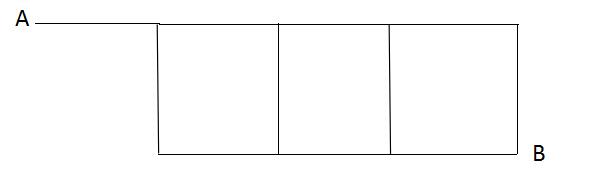
A.3 B.4 C.5 D.6
【答案】B。解析：要想A到B的路径最短，只能往右往下走，且不能走回头路。按照标数的步骤，起点标1，之后每一点上的标数等于与其相连的来路两点的标数之和，结果如下：
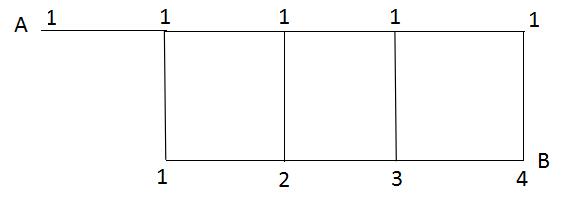
答案选择B。
在了解了标数模型的基本用法后，进入到今天最关键的环节，利用标数模型巧解排列组合问题中的公车换乘问题。
四、实际应用
【例2】从甲地到乙地含首尾共有15个公交站，在这些公交站上共有4条公交线路运行。其中，A公交车线路从第1站到第6站，B公交线路为第3站到第10站，C公交线路为第7站到第12站，D公交线路为第10站到第15站。小张要从甲地到乙地，要在这些公交线路中换乘，不在两站之间步行也不往反方向乘坐，每条公交线路只坐一次，则共有多少种不同的换乘方式?
A.72 B.64 C.52 D.48
【答案】D。解析：
第一种：常规解法。
A、B、C、D四条线路有交叉部分，换乘的方式主要有两类。
第一类，A到B到D。A到B可在第3、4、5、6站换乘(4种);B到D可在第10站换乘(1种);总的情况数为4×1=4种。
第二类，A到B到C到D。A到B可在第3、4、5、6站换乘(4种);若B到C在第7、8、9站换乘(3种)，则C到D可在第10、11、12站换乘(3种);若B到C在第10站换乘(1种)，则C到D可在第11、12站换乘(2种);总的情况数为4×3×3+4×1×2=44种。
分类相加，最终结果为4+44=48种。答案选择D。
第二种：标数模型。
我们利用数形结合的方式，将题干中小张换乘的所有路线用图形表示出来。
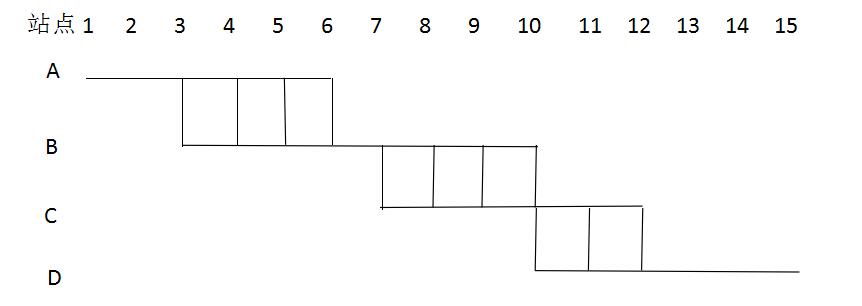
题干要求从A到D，换乘且不能往反方向乘坐，求换乘方式。从图中我们不难发现，换乘相当于从左到右、从上向下走，且不能反方向乘车。也就是要按一定方向从一点到另外一点，求路径数，因此我们这道题我们可以利用标数模型快速求解，解法如下：
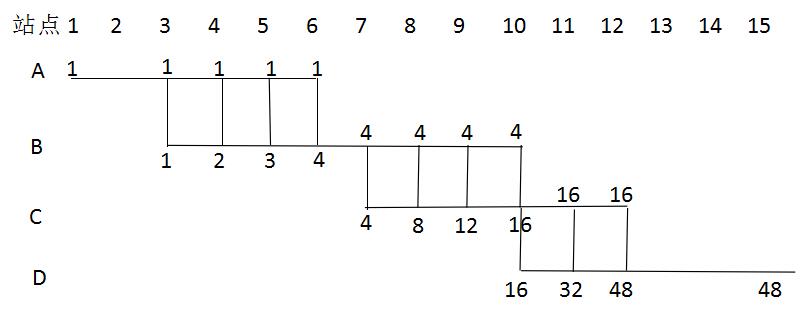
答案选择D。
申论太难没学会？扫码回复“咨询老师”
闂佸搫顦悧鎰涢崟顖涘仼闁绘劗鍎ら崕鎴澝归敐鍩挎帡宕戦幘璇茬闁挎梻鎳撴禍鎯归敐澶樻闁汇劍鍨甸埥澶愬箻绾惧顥濋悗瑙勬礈閸犳劙骞忛崨顓у悑闁割偅鑹炬禍楣冩煕閹伴潧骞樻俊鑼归湁婵犙冪仢閳ь剚鐗滅划濠囨晜閸撗咁槰闂侀潧鐗嗛幊鎰婵犳碍鐓涢柍褜鍓熷畷锝夊Ψ閵娿儱绠戦梻浣瑰缁嬫垿鎯夋總绋跨；闁挎繂顦粈鍕攽閻樺磭顣查柟宕囧█閺岀喖鎮€涙ê顏�闂備線娼уΛ鎾箯閿燂拷2025闂備胶枪濞存岸宕滃▎鎰弿闁绘梻鍘у婵囦繆椤栨瑨顒熸俊顖氼儔閺岋綁顢旈崘鈺冦偘婵炲濮撮悧鎾诲箠閹捐绀冩い顓熷灦鏍￠梻浣稿悑濠㈡﹢宕妸鈺佺劦妞ゆ帒锕ョ€氾拷闂備礁鎲″缁樻叏閹绢喖鐭楅柛鈩冪懅缁€鍐煏閸繄澧旈柛鐘诧躬閺屻劌鈽夊Ο鍨伃閻熸粍婢樺鍓佺矉瀹ュ鏁冮柕蹇曞Х缁夘剟姊虹粙璺ㄧ缂佸鍏樺畷褰掑磼閻愭潙娈屾繛杈剧到閹芥粓鎮烽敓锟�1闂佽娴烽。顕€骞忛敓锟�1闂佽崵鍠愰悷杈╁緤閸ф鍋ら柣鏃傚帶鐎氬鈧箍鍎遍幊搴綖閵堝鐓ユ繛鎴炃圭€氫即鏌涘Ο绋库偓妤呭箯绾懌浜归柟鐑樼箖濞堫參姊洪崨濠勬噭闁绘鍋熺划锝呂熺亸鏍т壕闂侇偅绋栭崗灞剧箾閹捐泛鍘撮柟铏崌瀹曟﹢鍩為悩杈╃獢妤犵偛绻橀幃銏犵暋閹殿喓鍋ｉ梻浣瑰缁嬫垿鎳熼姣椽寮介鍌滄澑闂佺硶鍓濋悷銉┿€傛總鍛婂仯闁搞儯鍔嶇粈瀣亜閿濆嫮鐭欑€规洩绻濆畷娆撳Χ閸モ晩妲烽梻浣呵圭换鍫ュ礉瀹€鍕┾偓鍐ㄢ堪閸涱垳鐣堕梺鍝勫暙濞层劌危閹间焦鈷掗柛顐ｇ☉閻忛亶鏌ｉ敂璇茬仸鐎殿噮鍋嗛埀顒勬涧閹诧繝宕愰悙鐑樺仯鐟滃秶鈧凹鍙冨鎼佹晸閻樿櫕娅栭梺璺ㄥ櫐閹凤拷
点击分享此信息：
相关文章
